daatelecom.blogg.se - Stepwise regression excel for mac

It looks as if the strongest relationship exists between either y and x 2 or between y and x 4 - and therefore, perhaps either x 2 or x 4 should enter the stepwise model first. You can get a hunch of which predictors are good candidates for being the first to enter the stepwise model. Now, if you study the scatter plot matrix of the data: Predictor x 3: % of tetracalcium alumino ferrite.

Predictor x 2: % of tricalcium silicate.

Predictor x 1: % of tricalcium aluminate.

Response y: heat evolved in calories during hardening of cement on a per gram basis.

Therefore, they measured and recorded the following data ( cement.txt) on 13 batches of cement: Sounds interesting, eh? In particular, the researchers were interested in learning how the composition of the cement affected the heat evolved during the hardening of the cement. Let's learn how the stepwise regression procedure works by considering a data set that concerns the hardening of cement.

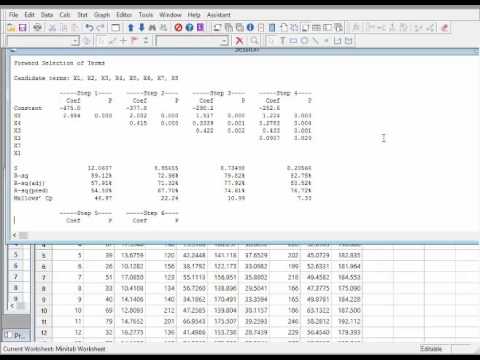
Otherwise, we are sure to end up with a regression model that is underspecified and therefore misleading. This leads us to a fundamental rule of the stepwise regression procedure - the list of candidate predictor variables must include all of the variables that actually predict the response. There is one sure way of ending up with a model that is certain to be underspecified - and that's if the set of candidate predictor variables doesn't include all of the variables that actually predict the response. Our hope is, of course, that we end up with a reasonable and useful regression model. While we will soon learn the finer details, the general idea behind the stepwise regression procedure is that we build our regression model from a set of candidate predictor variables by entering and removing predictors - in a stepwise manner - into our model until there is no justifiable reason to enter or remove any more. In this section, we learn about the stepwise regression procedure.